Le plus grand nombre premier connu identifié par un mathématicien amateur

La famille des nombres premiers vient de s’agrandir grâce à la contribution d’un chercheur amateur : dites bonjour à 2^136279841 – 1, un monstre qui s’étend sur 41 millions de chiffres !

Les nombres premiers sont des nombres entiers qui n’admettent que diviseurs, à savoir 1 et eux-mêmes. Cette particularité pourrait sembler anodine, mais cela en fait des objets mathématiques éminemment importants. En pratique, on peut les considérer comme les constituants fondamentaux de tous les entiers naturels — d’où leur nom.

À cause de ce statut particulier, les nombres premiers fascinent les mathématiciens depuis des millénaires. L’illustre Euclide, par exemple, a réussi à prouver il y a 2300 ans déjà qu’il existe une infinité de nombres premiers. Plus récemment, ce sont d’autres titans de la science comme Euler qui ont repris le flambeau, alimentant un champ de recherche dont la complexité a augmenté à une vitesse vertigineuse au fil des siècles. Et il ne s’agit pas que d’une expression abstraite. Gauss, un autre monstre sacré de la discipline, a notamment prouvé au 19e siècle que les nombres premiers deviennent de moins en moins fréquents à mesure que les nombres augmentent ; plus on avance dans la numération, plus ils deviennent rares.

Au-delà de la curiosité scientifique, les nombres premiers jouent un rôle crucial dans plusieurs branches de la science moderne. On peut citer les mathématiques fondamentales, notamment à travers ce qu’on appelle la théorie des nombres, mais aussi des disciplines plus concrètes, de l’informatique à la cryptographie.

2000 ans de quête mathématique

Les premiers nombres premiers, comme 2, 3, 7 et 5, ont été découverts de manière empirique en éliminant progressivement les autres nombres grâce à des algorithmes implémentés entièrement à la main. Eratosthène, que vous connaissez peut-être pour sa méthode qui permet d’estimer le diamètre de la Terre, a par exemple créé le Crible d’Eratosthène, un algorithme remarquablement efficace pour y parvenir 200 ans avant notre ère.

Mais à cause de la raréfaction mentionnée plus haut, cet exercice est devenu de plus en plus difficile. La chasse aux nombres premiers est donc devenue l’apanage de grands théoriciens comme Euler et Gauss — encore eux —, qui ont développé des méthodes encore plus sophistiquées pour comprendre leur distribution. Mais même ces génies ont fini par se heurter à un mur ; ils sont arrivés à un stade où il serait pratiquement impossible de trouver d’autres nombres premiers à la main.

Pour aller plus loin, il a fallu attendre l’arrivée d’un outil révolutionnaire : l’ordinateur. La montée en puissance de l’informatique correspond en effet à une accélération dramatique du processus. Par exemple, au début du 20e siècle, le calcul des nombres premiers se limitait à quelques millions ; dans les années 1960, les ordinateurs avaient déjà repoussé cette limite à plus d’un milliard, et ce chiffre n’a fait qu’augmenter jusqu’à aujourd’hui.

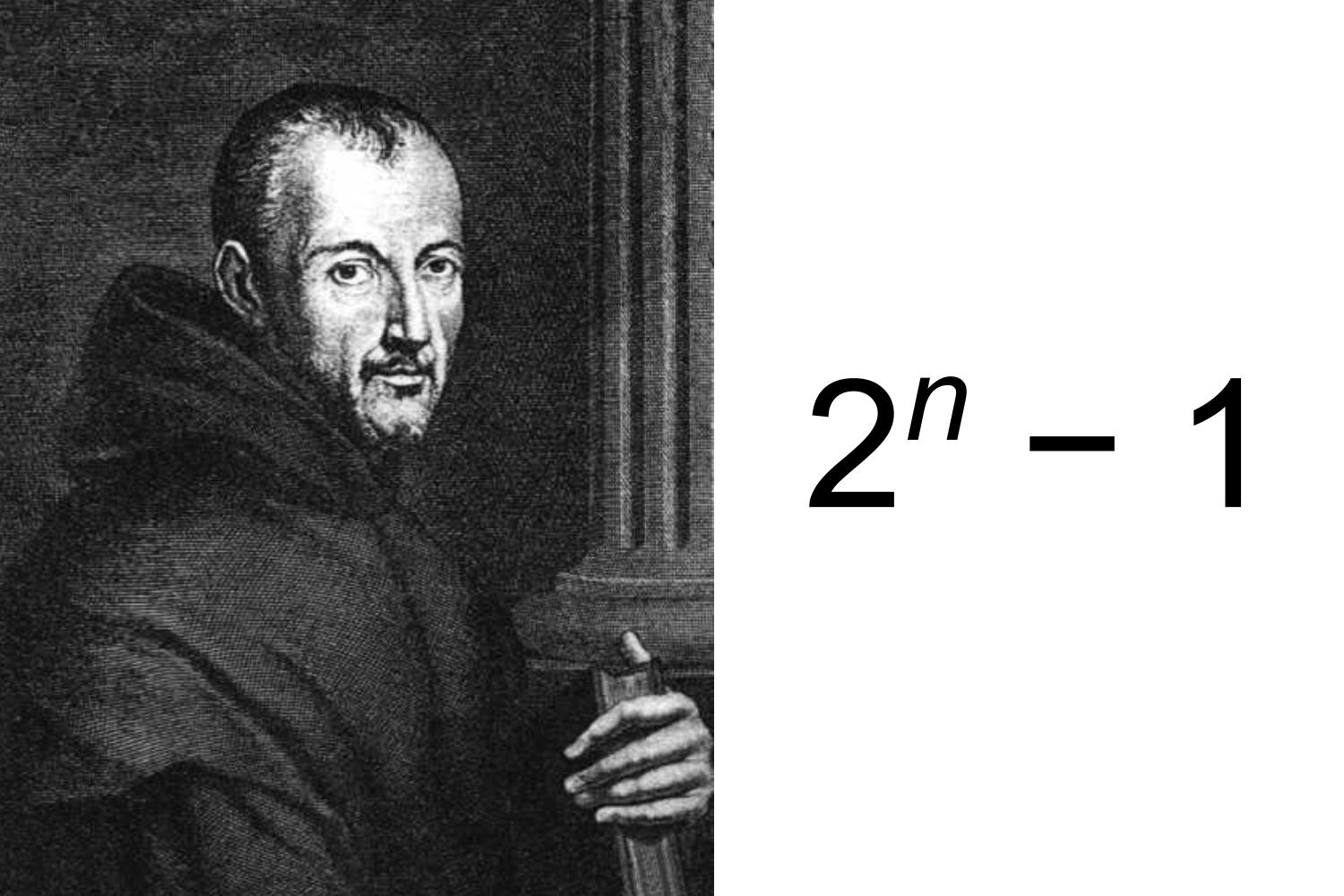
Cette tendance, on la doit notamment à une catégorie particulière de nombres premiers : les nombres de Mersenne, de forme 2 n − 1. Ces derniers ont été découverts dès le XVIIe siècle par le moine et mathématicien français du même nom. Mais leur importance n’a explosé que dans les années 70, quand les spécialistes ont réalisé que leur calcul implique des opérations qui peuvent être implémentées de manière particulièrement efficace par les ordinateurs.

Le début d’une nouvelle ère

La majorité des nouveaux nombres premiers découverts depuis ce grand tournant sont donc des nombres de Mersenne. Aujourd’hui, il existe des initiatives qui sont entièrement dédiées à leur traque. On peut notamment citer GIMPS (Great Internet Mersenne Prime Search). Il s’agit d’un projet collaboratif à travers lequel n’importe qui peut apporter sa pierre à l’édifice; il suffit de mettre sa machine personnelle au service de ces calculs en téléchargeant un logiciel open source appelé Prime95. En 2018, cette approche a d’ailleurs permis de découvrir ce qui était alors le plus grand nombre premier connu, sans utiliser le moindre supercalculateur.

C’est là qu’intervient Luke Durant, un ancien employé d’Nvidia qui est devenu un contributeur majeur de GIMP. Conscient du potentiel de calcul des GPU à cause de son parcours professionnel, il a introduit une nouvelle approche basée sur ces composants qui lui a permis d’identifier le 52e nombre de Mersenne, noté 2^136279841 – 1.

La validation de ce monstre à 41 millions de chiffres (16 millions de plus que le précédent, et de quoi remplir environ 11 000 pages A4 en police 12 !) marque donc un changement de paradigme. D’après la fondation GIMPS, elle « met fin au règne de 28 ans des ordinateurs personnels ordinaires dans la recherche de ces énormes nombres premiers » et lance une nouvelle ère placée sous la bannière de l’informatique haute performance.

En prenant un peu de recul, on peut s’interroger par rapport à l’intérêt de ces efforts ; cela vaut-il vraiment la peine de calculer des nombres premiers toujours plus énormes ? Au risque d’en frustrer certains, la réponse n’est pas totalement tranchée. À Force est de constater qu’à l’heure actuelle, il y a « peu d’utilisations pratiques pour ces grands nombres premiers », comme l’explique le communiqué de GIMPS.

Mais ce même billet souligne aussi le fait que « ces mêmes doutes existaient il y a quelques décennies, jusqu’à ce que d’importants algorithmes de cryptographie soient développés sur la base des nombres premiers ». Il est donc tout à fait possible qu’un jour, de nouvelles innovations fassent appel à ces nombres gargantuesques. Le cas échéant, nous pourrons donc remercier Durant et tous les autres acteurs de GIMPS qui vont continuer de réaliser ce travail de manière prophylactique !

🟣 Pour ne manquer aucune news sur le Journal du Geek, abonnez-vous sur Google Actualités. Et si vous nous adorez, on a une newsletter tous les matins.